 Welcome to the first in a series of articles on some basic battle mechanics in the Hobbit | KoM. In this series, we are gonna look at how combat in KoM basically works, and how it affects your gear choices. In this first part, we start of with looking at the basic battle formula, and work from there towards choosing the best gear set-ups, emphasizing primarily the reasons behind the sets such as given in the Best Sets article.
Welcome to the first in a series of articles on some basic battle mechanics in the Hobbit | KoM. In this series, we are gonna look at how combat in KoM basically works, and how it affects your gear choices. In this first part, we start of with looking at the basic battle formula, and work from there towards choosing the best gear set-ups, emphasizing primarily the reasons behind the sets such as given in the Best Sets article.
- Other parts in this series:
- 1. The basics
- 2. Adding in buffs
- 3. Adding in debuffs
- 4. Rewriting and final formula
>continued
In this first article, we are gonna construct the basic battle formula, starting with the most simple form of it, and slowly working towards the complete formula. This is in fact the foundation on which combat in KoM rests. Combat in KoM is actually rather simple: Two armies are pitched against each other, and combat works in rounds. Each round, both armies calculate the damage they can do, which is then assigned to the opposing army simultaneously for both sides. There is no first attack advantage, no range variations, no random factors such as critical hits. All very basic. Troops have an Attack and Life value, and basically the only things changing these numbers are the players’ buffs, and the strong/weak-against bonuses troops have over other troop types (foot> mounted> ranged> foot…).
Note that I will not be taking this last bonus into account in this series. This is because (1): It will make things really complicated, and (2): It is not necessary for the topics at hand. Such a detailed discussion would only be needed when we want to construct a battle simulator to predict combat outcome, such as needed for calculating Campaign battle outcomes and subsequent High Scores. This might be touched upon in a future series. But for now, back to the topic at hand: the basic battle formula.
1. The basics
 Let’s start with the basics. As combat is fought in rounds in which all damages are dealt simultaneously, each round of combat will involve two battle formulas: 1 to see how many troops you kill, and 1 to see how many troops your opponent kills. These two are both identical in form but totally separated from each other. In most situations, you will only focus on one of both.
Let’s start with the basics. As combat is fought in rounds in which all damages are dealt simultaneously, each round of combat will involve two battle formulas: 1 to see how many troops you kill, and 1 to see how many troops your opponent kills. These two are both identical in form but totally separated from each other. In most situations, you will only focus on one of both.
When attacking a city, your opponent is usually much larger and you only care how much enemy troops you kill, not how much the enemy kills, because that is going to be 100% in virtually all cases. Conversely, when defending, you only want to focus on how many troops the opponent kills.
Let’s say you are defending your city. You have 100 troops with 1 Life. An attacker comes along who has 20 troops with 1 Attack. How many troops does he/she kill? Without extra buffs, the attacker will kill 20 troops of your army. Whether we state this as (20/100)*total_troops, or 20/1 (Life per troop), the basic formula is:
The amount of troops killed (TK) is equal to Attack divided by Life. From this basic first formula, we can start adding in buffs and debuffs, to figure out what exactly those “Att” and “Life” factors are.
2. Adding in Buffs
To do this, I will focus on the attack factor right now. Mind you that both factors in (eq. 1) are identical, and the worked out Life factor will be added in again later. For now we are going to expand and form just the “Att” factor.
 So what is attack? It starts with the attack value of your troops. This will be a solid constant, that only changes depending on what troops we are discussing, which we will skip here as well. As far as we are concerned, all troops of the same type and tier have the same base attack values.
So what is attack? It starts with the attack value of your troops. This will be a solid constant, that only changes depending on what troops we are discussing, which we will skip here as well. As far as we are concerned, all troops of the same type and tier have the same base attack values.
Buffs are meant to increase whatever they buff, be it attack, life, or resource production. A 100% attack buff will double your attack (base * 2). 200% Attack buff will triple your attack (base * 3), and so on. Stated mathematically, this looks as follows:
The “1+” term makes sure the end product will never be zero, so 0% attack buff still means we have our base attack value. In this formula, percentages are divided by 100. It should now be clear that a 100% attack buff means the base attack value is multiplied by (1+1)=2.
3. Adding in debuffs
 Now that we have covered buffs, it is time to look at debuffs. Debuffs can, for some, be a bit counter-intuitive. Many people still wonder what a 100% attack debuff does. Does it completely negate the enemy attack? And what if you go over 100% debuff? Is there a cap? The answer is actually pretty simple: If a 100% attack buff multiplies attack by 2, a 100% debuff simply divides it by 2.
Now that we have covered buffs, it is time to look at debuffs. Debuffs can, for some, be a bit counter-intuitive. Many people still wonder what a 100% attack debuff does. Does it completely negate the enemy attack? And what if you go over 100% debuff? Is there a cap? The answer is actually pretty simple: If a 100% attack buff multiplies attack by 2, a 100% debuff simply divides it by 2.
Once again the “1+” term ensures the math works out even at 0% debuff, and 100% debuff translates to division by (1+1)=2.
4. Rewriting and final formula
We pretty much have right now all that is needed to construct the final battle formula. First we need to combine buffs (eq. 2) and debuffs (eq. 3):
To make this part easier to work with for now, we can move the buff factor on the right to the base attack numerator on the left following this rule:
Which gives the following formula for calculating total attack:
As I’ve stated, the math behind the “Life” factor in (eq. 1) is identical to the “Att” factor, so following the same steps above, we come to this:
Now we need to substitute (eq. 6) and (eq. 7) into the original formula (eq. 1), giving us the following formula:
For all intends and purposes we are done now, but we have a division divided by a division, so I am gonna move that around to get rid of the main division. Again following a simple math rule:
We can multiply the “Att” and “Life” terms simply by switching the two factors in the “Life” factor division, as shown in (eq. 9). This gives us, for now, the final formula:
This formula contains everything we need to know about a KoM combat situation. Note that as I have said in the introduction, when you attack another player or Goblin camp, or you are being attacked, 2 sets of these formulas are used: one to calculate the troops you kill in a given combat round, and one to calculate how many troops the opponent kills. After each calculations, the troop kills are subtracted from each army, and as long as both armies still have troops standing, combat will go on to the next round.
Because this same formula is used for both defending and for attacking, I have made one final adjustment to (eq. 10), by coloring in the buffs and debuffs belonging to each player:
Depending on your situation, your buffs will comprise either the blue factors or the orange ones. If your buffs and debuffs are the orange factors, you are attacking, and the result of the formula, if you would know all numbers involved, would tell you how many enemy troops you kill. If your buffs comprise the blue factors, you are looking at your defensive capabilities, and the formula would give you (ideally) how many troops the enemy kills, or how many of your troops will be lost.
For most PvP situations, this is impossible as you do not know the enemy’s buffs and debuffs exactly (although approximations can be made on the basis of battle reports). But this does not make it useless, and in fact this formula is still highly valuable.
For one, we can still calculate relative effectiveness in combat, be it PvP or PvE. While absolute effectiveness would tell you exactly how many enemy troops you would kill in PvP, relative effectiveness can state that wearing a certain set of gear will triple your TK’s compared to the base value. This means that (eq. 11) can still be used to assess which sets of gear perform best in certain situations. Secondly, as mentioned, the formula does work out for campaign, precisely because we DO know the enemy buffs and debuffs, as Goblins have no gear/debuffs etcetera.
In part III of this series we are gonna look closer into this relative effectiveness mentioned earlier, but first, we need to take one step back and take a second look at the Attack and Life buff factors. See you in part II.



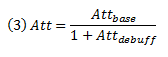





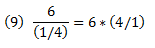


Has it been verified that a 100% attack debuff divides the attack base by 2? I thought that a 100% attack debuff completely wipes out the attack base. I have not tried this yet, but if I was right, the attack formula would then look like this: Att = Att base * (1 + Att buff – Att debuff). In such case, if both buff and debuff are 100%, they cancel out, and the remaining is the Att base.
In similar sense, the life formula would look like: Life = Life base * (1 + Life buff – Life debuff).
It would be good to know if someone has verified any of the formula presented in your post, or in this comment. Thanks.
LikeLike
Pingback: Battle Mechanics – Steel Floss
Pingback: w5840
Recently i sent in a ticket to Kabam because of a battle i had at a cavern. My hero, gear and buffs were far superior & troops well matched. With that being said i lost this battle and couldn’t understand what just happened. Kabams response was that there were random calculations for the defender but no specifics were given. Is there any way you can shed some light on this? If this is true then your calculatios, while appreciated, mean nothing. (No disrespect whatsoever to you, BM)
Needless to say i was slightly beside myself, scratching my head, trying to make sense of what i was just told. I can send you a CC of Kabams reply to my ticket if you’d like.
LikeLike
In caverns, the defender does not have the high ground, or in essence, the defender is not defending the cavern, but attacking. The person with the higher attack buffs almost always win in caverns
LikeLike
Absolutely wonderful post! Been working on something similar myself. In fact, I’m working on the breakpoint of DR buffs versus troop count and how they can effect each other. Nice to see some of my work verified by someone else,
LikeLike
Excellent! Good to see this series starting. The formulas, for relative purposes, can actually be simplified a little more — but more formulas and simplifications would complicate things… and I think you’ll cover that in the next part, why the opponent doesn’t matter. 🙂
LikeLike
exactly, so thank you for your patience 🙂
LikeLike